Temperature, Mortality and Climate Change

Antonio Gasparini et. al. 2015 is an article in Lancet estimating global mortality from heat and cold, using an elaborate statistical process¹ applied to an enormous collection of data, more than 74 million deaths across 384 locations in thirteen countries. It found mortality from cold, from temperatures in each place below that at which mortality was minimized, to be much larger, about seventeen times as large, as mortality from heat, similarly defined. It also found that mortality from both heat and cold was not mainly due to extreme temperatures, heat waves and cold waves, but to less extreme temperatures above or below the optimum.

More temperature-attributable deaths were caused by cold (7.29%, 7.02–7.49) than by heat (0.42%, 0.39–0.44). Extreme cold and hot temperatures were responsible for 0.86% (0.84–0.87) of total mortality.

Antonio Gasparini et. al. 2017 is an article that estimates the mortality effect from warming due to climate change over the rest of this century, combining the IPCC projections of temperature change by country under four different emissions scenarios (RCP2.6, RCP4.5, RCP6.0, and RCP8.5) with the earlier article’s approach to measuring the effect of temperature on mortality.

Results indicate, on average, a net increase in temperature-related excess mortality under high-emission scenarios, although with important geographical differences. In temperate areas such as northern Europe, east Asia, and Australia, the less intense warming and large decrease in cold-related excess would induce a null or marginally negative net effect, with the net change in 2090–99 compared with 2010–19 ranging from −1.2% (empirical 95% CI −3.6 to 1.4) in Australia to −0.1% (−2.1 to 1.6) in east Asia under the highest emission scenario, although the decreasing trends would reverse during the course of the century. Conversely, warmer regions, such as the central and southern parts of America or Europe, and especially southeast Asia, would experience a sharp surge in heat-related impacts and extremely large net increases, with the net change at the end of the century ranging from 3.0% (−3.0 to 9.3) in Central America to 12.7% (−4.7 to 28.1) in southeast Asia under the highest emission scenario.

The conclusion appears surprising; warming due to climate change should reduce mortality from cold as well as increasing that from heat and total mortality from cold is, according to the earlier article, much larger than from heat. Further, greenhouse warming tends to be greater in cold times and places than in warm, which should bias the effect in favor of a reduction in mortality.

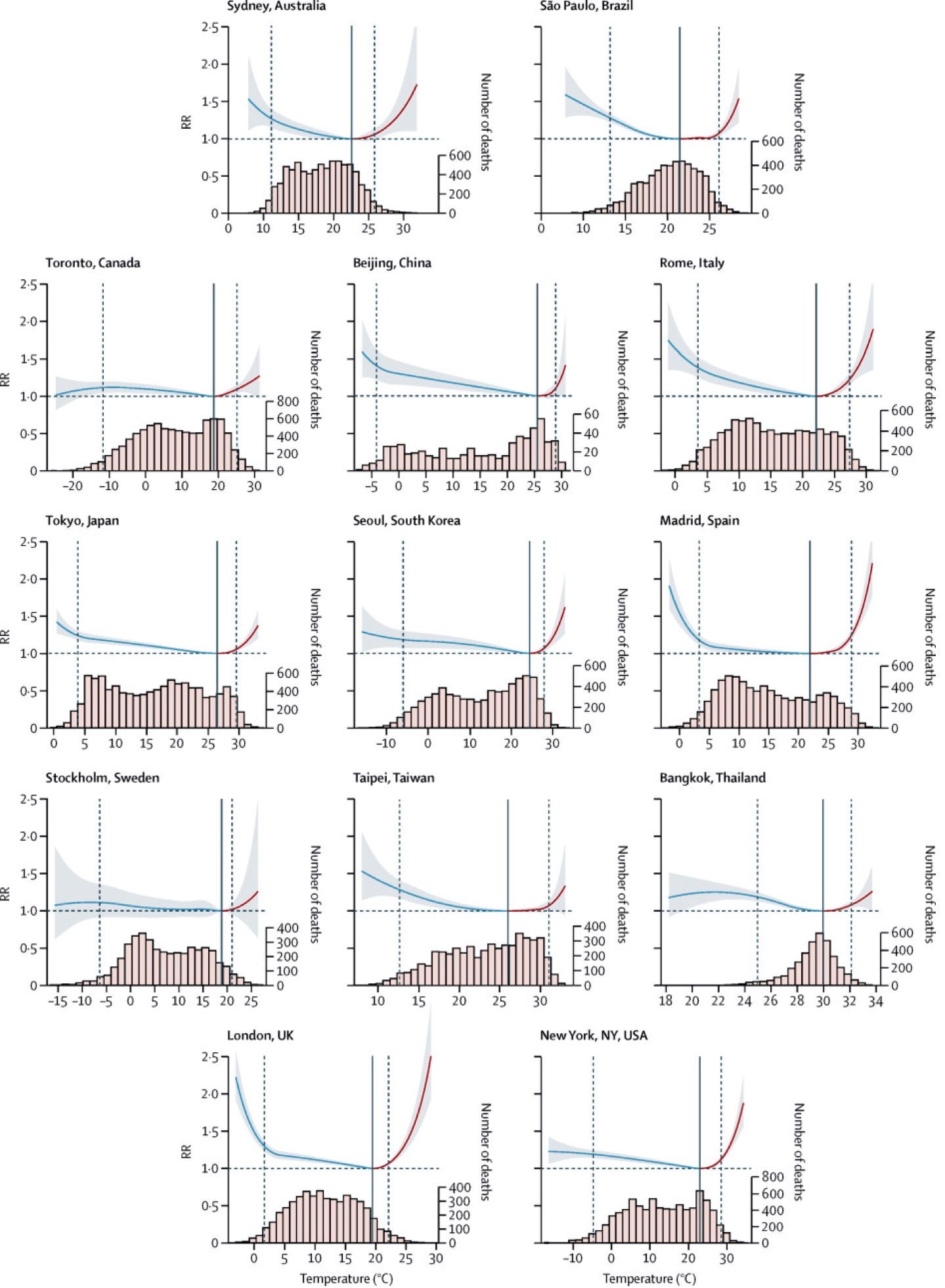
Figure 1 from the earlier article suggests a possible explanation; mortality rises much faster for temperatures above MMT (Minimum Mortality Temperature) than it falls for temperatures below, especially for temperatures several degrees above. While that is a possible explanation I still find the result surprising.

Figure 1: Overall cumulative exposure–response associations in 13 cities

One possible problem:

We projected excess mortality for cold and heat and their net change in 1990–2099 under each scenario of climate change, assuming no adaptation or population changes. (Gasparini et. al. 2017)

The assumption of no adaptation implies that the relation between temperature and mortality will be the same after most of a century of warming as it was initially. That cannot be correct. A Chicago winter in San Jose would kill a lot more people relative to the population than it does in Chicago, since people in San Jose have lighter clothing, less well insulated and heated housing than people in Chicago. A Tucson summer in San Jose would kill more people, relative to the population, than it does in Tucson, for similar reasons. The article’s calculation simply assumes away everything that individuals do to adjust their lives to their environment.

It is possible to use the article’s results to take account of adaptation, although imperfectly. Looking at the graphs in Figure 1, mortality in each city is more nearly a function of the deviation of temperature, positive or negative, from that city’s Minimum Mortality Temperature than it is of the absolute temperature. If we assume that mortality in each city is a function of the deviation of temperature from its optimum it follows that if climate change raises the average temperature of a city by three degrees and MMT for that city by one degree the effect on mortality will be the same as if it raised the average by two degrees with no effect on MMT.

To estimate the effect of climate change on MMT I used the observed relation between average temperature and MMT across cities, assuming that it will be the same across time as across space. Figure 2 shows the relation;² as one would expect, MMT increases with average temperature. A least squares fit to the data finds a slope of .41; on average, MMT goes up .41° for every degree increase in average temperature. It follows that we can estimate the effect on mortality with adaptation by reducing the temperature increases used in the article accordingly, replacing a temperature increase of ∆T due to climate change with an increase of .59∆T.

Figure 2: Scatter plot

That result let me use the information in the second article to correct the article’s mortality results to allow for adaptation. If, to take a simple example, the corrected temperature for North America at the end of the century under RCP 8.5 is halfway between the uncorrected temperature for RCP 8.5 and the uncorrected temperature for RCP 6.0 then the corrected mortality figure should be about halfway between the mortality figures for the two emission paths. Generalizing that, I can find for any region, date and RCP the corrected temperature and the linear combination of uncorrected temperatures, typically of that RCP and the next lower one,³ that gives the same value. I then calculate the linear combination of mortalities reported in Table S1 of the article using the same weights and use that as my estimate of the corrected mortality.

Table 1 shows mortality results by region and emission path both from Table S1 and corrected for adaptation as described above for the middle of the century, Table 2 for the end of the century, both based on Table S1 of the article.

Under RCP8.5 climate change by mid-century decreases mortality  in four of the nine regions, increases it in four, in both the uncorrected and corrected versions. By the end of the century it decreases in two in the uncorrected version, three in the corrected.

RCP 8.5 was originally designed as an upper bound to plausible emissions, what happens if everything that can go wrong does, so I take RCP6.0 as a plausible guess at future emissions assuming nothing major is done to hold them down. Under RCP 6.0 climate change by mid-century decreases mortality  in five of the nine regions, increases it in four. By the end of the century it decreases in four, increases in five. The correction for adaptation affects the size of the changes but not their signs. Under RCP4.5, a more optimistic guess at future emissions, the correction increases the number of regions where mortality falls by the end of the century from four to five.

What about the total effect? To estimate that, I multiply the effect in each region by the region’s population. That isn’t exactly right, since the effect is a change in mortality due to temperature measured (I believe) as a percentage of total mortality, and mortality will be different in different regions, but I don’t have the data to take account of that. The result is a decrease in total mortality by mid-century, a significantly larger increase by the century’s end.

What Are They Measuring?

In addition to the failure to take account of adaptation (or migration) there is a second very serious problem:

We modelled the non-linear and delayed exposure–lag–response relationship between temperature and mortality with a distributed lag non-linear model, applying a bidimensional cross-basis spline function with 21 days of lag.

What is being estimated in both articles is the effect of one day’s temperature on the number of people who die during the next 21 days. Including a 21 day lag avoids overestimating the mortality effect of one day’s heat or cold by counting someone who dies that day but would have died anyway a few days later — the “harvesting” effect.

But it provides no way of telling whether the additional death is of someone who would have died a month later or would have lived for another forty years. That is information is needed to convert the effect of warming on mortality to a cost to be included with other costs and benefits of climate change, as is done in (for example) Rennert et. al. 2022, discussed in an earlier post. If the reduction in mortality due to cold prevents deaths of people who  would otherwise live for another twenty years and the increase in mortality due to heat prevents deaths of people who would otherwise live for ten, the net effect could be an increase in average life span even if the increase in deaths was greater than the decrease, a net benefit not a net cost.

If the data used in the articles included the age of each person who died we could make a first cut at the problem by assuming that, absent temperature related mortality, each person would have the average lifespan. I gather, from correspondence with Gasparini, that he has such data for some cities although not for his whole sample so could, perhaps will, see if deaths from cold are, on average, older or younger than from heat.

What is Left Out

The article takes no account of progress in either medical technology or the technologies used to protect against heat and cold, most obviously heating and insulation. It takes no account of reductions in the effect of temperature on mortality due to rising incomes. Both can be expected to reduce the size of the mortality changes but not necessarily their sign, since they will reduce both the increased mortality from heat and the decreased mortality from cold.

1. Curious readers should read the article for a description of how the data were analyzed.

2. Neither article shows the average temperature of the cities. I used Temperature data from University of East Anglia Climatic Research Unit; Harris, I.C.; Jones, P.D.; Osborn, T. (2022): CRU TS4.06: Climatic Research Unit (CRU) Time-Series (TS) version 4.06 of high-resolution gridded data of month-by-month variation in climate (Jan. 1901- Dec. 2021). NERC EDS Centre for Environmental Data Analysis, date of citation. https://catalogue.ceda.ac.uk/uuid/e0b4e1e56c1c4460b796073a31366980

3. In some cases the adjusted temperature is below the unadjusted temperature for the next lower RCP, so I have to use the linear combination of unadjusted temperatures for the next lower RCP and the one below it. For the lowest RCP, RCP2.6, I calculated the corrected mortality as uncorrected mortality times corrected temperature change/uncorrected temperature change.