Temperature, Income and Mortality

Mining Gasparini 2015 to improve on Gasparini 2017

In a recent post I discussed a pair of related Lancet articles, the first on the effect of temperature on mortality, the second on the effect of climate change on mortality via its effect on temperature. There are two problems with the second article, Gasparini et. al. 2017, that I believe I can use the articles’ data to partly fix, and a third that I believe the lead author might be able to reduce with data available to him.

Adaptation

The first problem, discussed in my earlier post, is that Gasparini et. al. 2017 does not take account of adaptation, of people adjusting their behavior in response to long term changes in temperature. Its calculations, as best I understand them, assume that the relation between temperature and mortality will be the same after climate change has warmed a city by several degrees as it was in the recent past. That makes no allowance for people changing how well insulated their houses are, whether they have air conditioning, or their pattern of life in response to a century of warming.

My earlier post attempted to take account of such effects by seeing how MMT, the temperature that minimized mortality, varied with average temperature. Using that and the assumption that mortality depended not on the absolute temperature but on how much above or below MMT it was, I adjusted the second article’s estimate of the mortality effect of the increase in temperature implied by climate models with different emission scenarios. That is a very approximate way of taking account of adaptation but I think better than ignoring it.

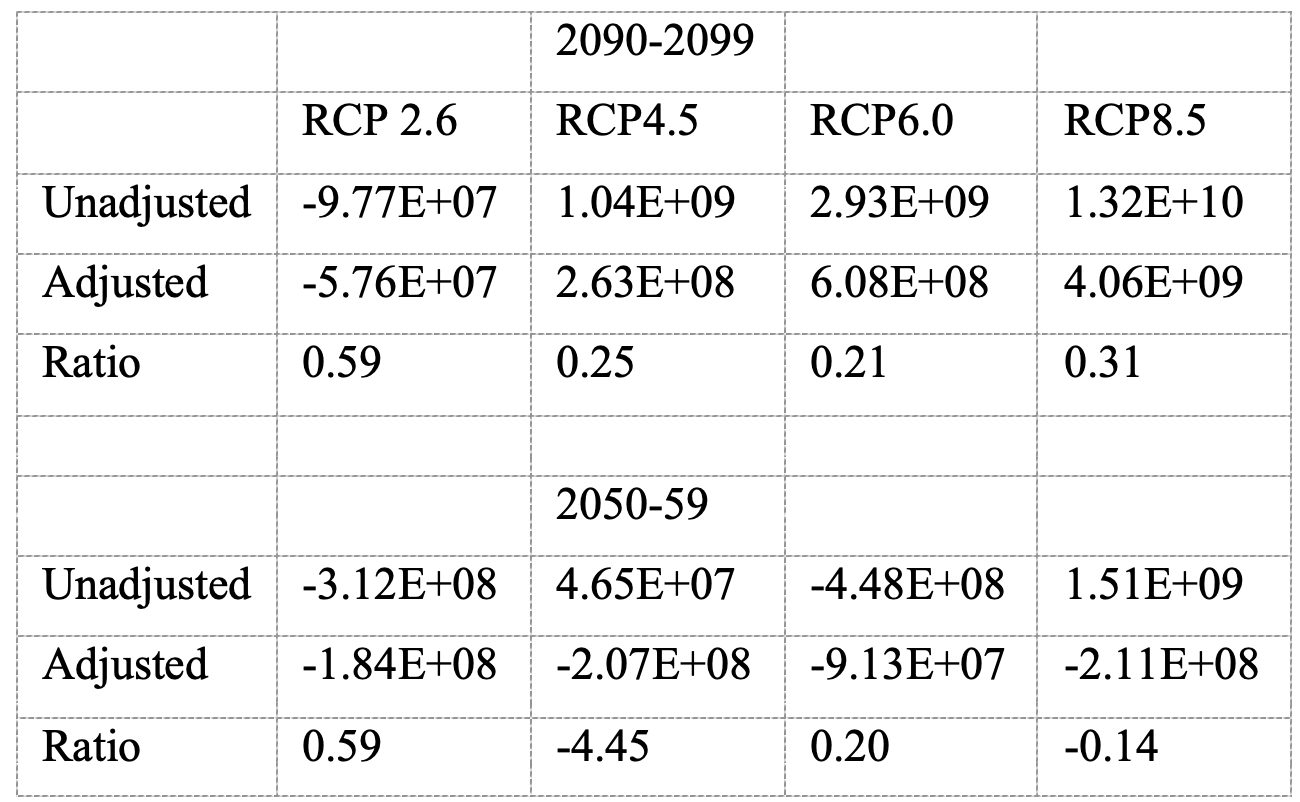
My earlier post reported the result as a percentage change in mortality at the middle and end of the current century for each emission scenario and region. I went on to calculate the effect on global mortality by adding up the effect on the regions weighted by each region’s population. Since I did not report that result in the earlier article I am doing so here. The numbers on the table are estimates of the percentage increase in mortality times population. The sign tells us whether the estimate is for an increase or decrease in mortality, the size gives an estimate of the relative effect on mortality of different emission paths or calculating with or without the adjustment for adaptation.

Adjusting the mortality figures to take account of adaptation does not change the sign of the effect  as of the end of the century; mortality still decreases due to climate change for RCP2.6, increases for the other three, but it substantially reduces the size of the effect, as shown by the ratio between the adjusted and unadjusted effects. In mid-century the unadjusted estimate shows a reduction in mortality for two of the four emission paths, an increase for two; the adjusted estimates show climate change reducing mortality for all four.

What about the effect for total mortality over the century, the integral of the annual mortality rate? If we interpolate with straight lines and calculate the area under them and use my adjusted figures, total mortality over the century is positive for RCP8.5 and RCP6.0, negative for RCP4.5 and RCP2.6.

Income, Temperature and Mortality

We would expect mortality due to either heat or cold to decrease with income, since rich people are likely to have better insulated houses and less need to go out in bad weather than poor. Gasparini et. al. 2017 ignores that effect in its calculation of temperature related mortality as does Rennert et. al. 2022, discussed in an earlier post. The latter article projects GNP per capita, and so presumably income, rising about three-fold by 2100, about eleven-fold by 2300.

What would we expect the effect of that  to be on temperature-related mortality?

Data in Gasparini et. al. 2015 can be used to give at least a rough answer to that question, assuming as with adaptation that changes over time  follow the same pattern as over space. Mortality by location (mostly cities) is shown in Table S4 of Gasparini 2015, average temperature in Harris et. al. I have not yet found a source of per-capita income for all locations in Table S4 but did find one online for almost all of the US locations.¹ With that data I can use a multiple regression with the change in net mortality  as the dependent variable, income per capita and average temperature as the independent variables, to see how mortality changes with income.²

I ran regressions both for the U.S. cities and for the full list of cities, in the latter case attributing to each city the average income of the country it was located in, both with income and log income as independent variables. My results:

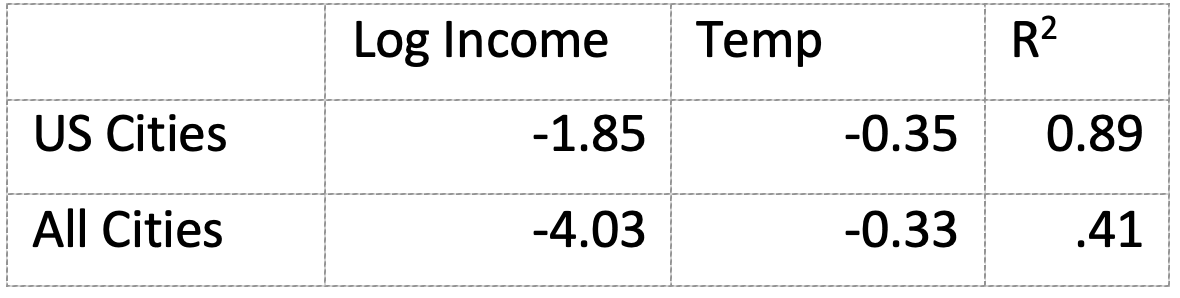
Using income and temperature as the independent variables, coefficients and R² are:

Using log income and average temperature, coefficients and R² are:

The regression coefficient for income lets me estimate how mortality would change for a fixed increase, say ten thousand dollars a year. The coefficient for log income lets me estimate the effect of multiplying everyone’s income by a fixed amount. Since the estimates for income change over time in Rennert, tripling by the end of the century, increasing eleven-fold by 2300, are of the latter sort, I used the log income figures to estimate their effect.

The regression coefficient on log income for US cities implies that tripling income will reduce the percentage increase in mortality by 1.85xlog3 = .9 . Since the average increase in mortality for the US cities is 5.76 that calculation suggests that Gasparini’s estimates of mortality by the end of the century should be reduced by about 15% to allow for the effect of the income increase and Rennert’s for mortality in 2300 by about 61%.

The all cities regression coefficient on log income gives a reduction, calculated inn the same way, by 1.9 for the end of the century, 4.2 by 2300. The average for all cities is 6.35, which suggests that the mortality figure for the end of the century should be reduced by about 30%, for 2300 by about 66%.

As I hope is obvious, these are very approximate estimates. The U.S. cities figure shows the effect of income on mortality for a rich, developed society; it might be quite different for China, India, or an African country.

The fact that the coefficient is much higher for the all cities regression could reflect a larger effect of income in poorer countries but it might also reflect the effect of using national income not city income; national income may be a proxy for other features of a country that affect mortality. One advantage of using cities from one country is that they are likely to vary less in ways other than income and temperature than cities in different countries.

These are very approximate estimates but, I think, better than nothing.

Mortality vs Years of Life Lost

What is being estimated in both Lancet articles is the effect of one day’s temperature on the number of people who die during the next 21 days. Including a 21 day lag avoids overestimating the mortality effect of one day’s heat or cold by counting someone who dies that day but would have died anyway a few days later — the “harvesting” effect. But it provides no way of telling whether a death is of someone who would have died a month later or would have lived for another forty years.  Hence it provides no way of knowing how many years of life are lost or gained due to the effect of climate change on temperature.

If the data used in the articles included the age of each person who died we could make a first cut at the problem by assuming that, absent temperature related mortality, each person would have the average lifespan. I gather from correspondence with Gasparini that he has such data for some cities so could, perhaps will, see if deaths from cold are, on average, older or younger than from heat.

Warming decreases deaths from cold, increases deaths from heat. If it turns out that cold kills older people than heat it might turn out that climate change increases temperature-related mortality as measured in the articles but decreases number of years of life lost. If cold kills younger people, on the other hand, the effect of warming is worse than the articles imply.

Technology

One other complication ignored by both Gasparini and Rennert is the effect on mortality of progress in technology, medical technology and technologies that affect the cost of temperature control. I have no good way of estimating the size of that effect but, in my post on Rennert, offered evidence from past reductions in mortality that it could be large.

P.S.

If anyone reading this knows of a source of data on per capita income or temperature variance by city that covers a large number of cities, let me know. Either would let me substantially improve my calculations. If anyone wants to duplicate my calculations and improve on them, perhaps by trying a wider variety of functional forms, I will be happy to send you my data. It is all from publicly available sources, mostly the Lancet articles, but it took some effort to put it together.

P.P.S.

A commenter points me at a news story on a recent study which finds that:

"Importantly, cold-related death decreased 0.51 per cent from 2000 to 2019, while heat-related death increased 0.21 per cent, leading to a reduction in net mortality due to cold and hot temperatures."

The headline of the news story and the beginning suggest the opposite:

World’s largest study of global climate related mortality links 5 million deaths a year to abnormal temperatures

08 July 2021

More than five million extra deaths a year can be attributed to abnormal hot and cold temperatures, according to a world first international study led by Monash University.

Deliberate dishonesty or poor reading ability?

Sorted links to my previous posts.

1. It showed income by metropolitan statistical area, sometimes including several cities. Where one metropolitan area included only one of the cities in Table S4 I attributed the income of the area to the city. Where it included two different cities on the table I found income figures online for each city and, if they were substantially different as in every case they were, eliminated those cities from my data. I could have looked up income online for each city separately but different sources for income data are not always consistent with each other.

2. I could do a better job if I had data on not only average temperature but variance of average temperature for each location, since temperature-related mortality probably depends on that as well. I may try to obtain such data in the future.